¿Eficaz? ¿RMS? ¿Pico? …
Si en alguna ocasión te has cruzado con una señal de tipo senoidal, seguro que te suena el famoso √2 de la tensión eficaz, también llamado tensión RMS. Cómo casi seguro sabrás, la señal senoidal se suele caracterizar por su tensión de pico o su tensión RMS o tensión eficaz.
La tensión de pico es la tensión máxima instantánea que alcanza la tensión, lo mismo ocurre con la corriente. La corriente de pico corresponde con el máximo valor de corriente instantánea que puede alcanzar.
El valor eficaz o también denominado valor rms, es un valor teórico que usamos para poder realizar multitud de cálculos, entre ellos los cálculos asociados a potencia.
![]()
Procedencia
La realidad es que podemos calcular la tensión eficaz de cualquier señal periódica y lo hacemos mediante la siguiente ecuación:
(1) 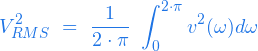
Se lo que estas pensando. ¡¡¡Integrar!!!! ¡¡¡Otra vez!!! La respuesta es que sí. Es por esto que es más fácil enseñar que si tenemos una señal senoidal, lo que debemos hacer es multiplicar o dividir por raíz de 2.
Un tensión senoidal se describe como:
(2) ![]()
Siendo Vp la tensión de pico de la tensión senoidal, ω la frecuencia angular y t el tiempo. Y por si te lo estás preguntando, ω = 2 π f siendo f la frecuencia de la señal en Hz
En el siguiente vídeo realizo el desarrollo de la ecuación (1) particularizada para la tensión de la ecuación (2).
Así que ya sabes de donde viene la ecuación del famoso raíz de 2.
Recuerda que puedes usarla siempre que tengas señales senoidales perfectas o casi perfectas. En caso de tener una señal senoidal deformada, usar raíz de 2 no es el mejor método, lo mejor es particularizar la ecuación (1).
Puedes continuar aprendiendo y averiguar de dónde viene la ecuación del divisor de tensión.



